(2023年8月31日作成)
本ページにおいては、土地に関する資料から、地積や距離を算出することについて、実務的なテクニック手順を解説しております
相続税の土地評価と聞くと実測するイメージが強いが、実は実測を必ず求められていない
国税庁のホームページの回答において、「実際の地積によることの意義」があります。
・土地の地積を「実際の地積」によることとしているのは、台帳地積(=固定資産課税台帳における地積=登記簿地積※)と実際地積とが異なるものについて、実際地積によることとする基本的な考え方を打ち出したものです。
・したがって、全ての土地について、実測を要求しているのではありません。
・特に縄延の多い山林等について、立木に関する実地調査の実施、航空写真による地積の測定、その地域における平均的な縄延割合の適用等の方法によって、実際地積を把握する
・台帳地積によることが他の土地との評価の均衡を著しく失すると認められるものについては、実測を行うこととなります。
※台帳地積は基本的には登記簿の面積が記載されていますが、国土調査法に基づく地籍調査などにより台帳地積と登記簿の地積が異なることがあるそうです。
以上より、実測を必ず求められていない、ということになります。
地積測量図などの寸法が信頼できる資料により地積や寸法を取得可能であれば、その寸法を利用すればよいことになります。
実際問題として更地は奥行距離を容易に直線距離を実測できるが、建物が立っている土地は壁などの障害物で容易に奥行直線距離を実測できない、つまり完全な実測はやろうとしても難しい
長方形、正方形の面積の計算式は、縦×横、とご存じだと思います。仮に長方形、正方形の土地であるとして、
・横=間口距離
・縦=奥行距離
とします。
あなたのご自宅の間口距離(横)を測ってみましょう。玄関をでて、道路に面している玄関の、ご自身の敷地の端から端までをメジャーをおいて測定できるでしょう。
次に、あなたのご自宅の奥行距離(縦)を測ってみましょう。玄関をでて、道路に面している玄関の敷地の最も端にメジャーを置くでしょう。しかしどうでしょうか、そのままメジャーの一方の端をもって、直進距離の奥行距離を測定可能でしょうか?ご自宅の柱や扉が邪魔ではないでしょうか?仮に迂回したとしても、正確な距離は測定不可能です。
ではどうするのでしょうか?
公図等の図面で縮尺がわかる場合
公図等の図面で「縮尺が明示されている資料」については、当該図面の寸法を採寸すれば、縮尺を乗じることで実測の推定値を推定可能です。
・縮尺が1/500の場合、公図での寸法が4cmであれば、500倍して100で割れば20mと換算できます。
縮尺不明の場合は実測の間口距離と公図等の間口距離との割合で、縮尺割合を算出する
公図等の図面で「縮尺不明の資料」については、実測の間口距離を測定し、公図等の間口距離の寸法との比率が縮尺割合となります。
・実測の間口距離が20mであり、公図等の間口距離の寸法が4cmであれば、4cm/2,000cmということで縮尺割合1/500となります。
三斜面積計算で地積を算出する
(図1)三斜面積計算
ここで小学校の図形計算の知識を思い出しましょう。
・長方形の面積=正方形の面積=縦×横
・平行四辺形の面積=底辺×高さ
・台形=(上底+下底)×高さ÷2
・三角形の面積=底辺×高さ×1/2
となります。
ただ、不整形の土地の形状は、上記のいずれの形でもない場合があります。その場合の面積の計算方法はどうするのでしょうか?
(図1)のように三斜面積計算という方法を用いて計算します。図形を三角形に分解して、それぞれの三角形の面積を求めて合計する方法となります。
公図から三斜面積計算を用いて地積を算出する手順
(図2)公図をコピーしたもの
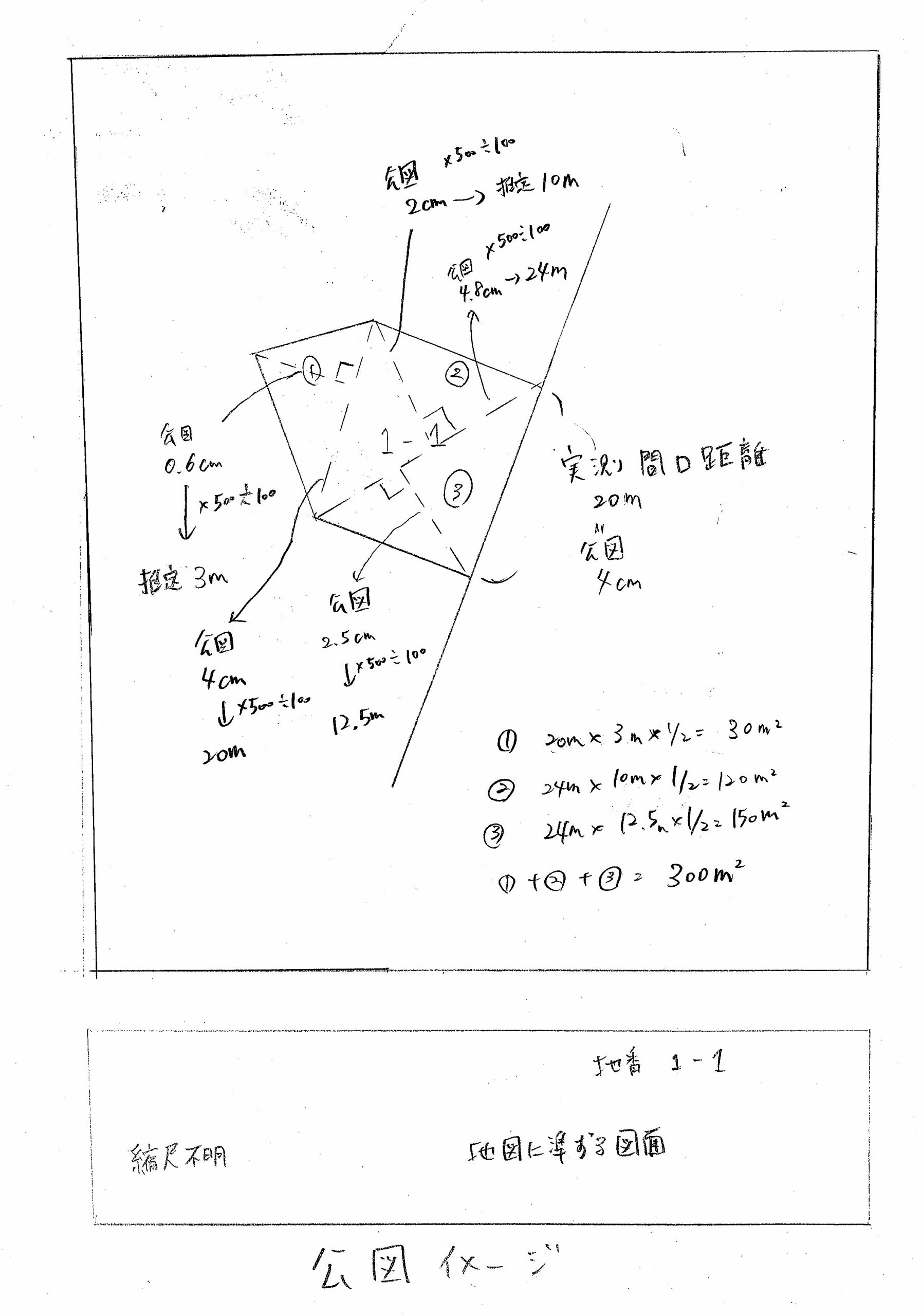
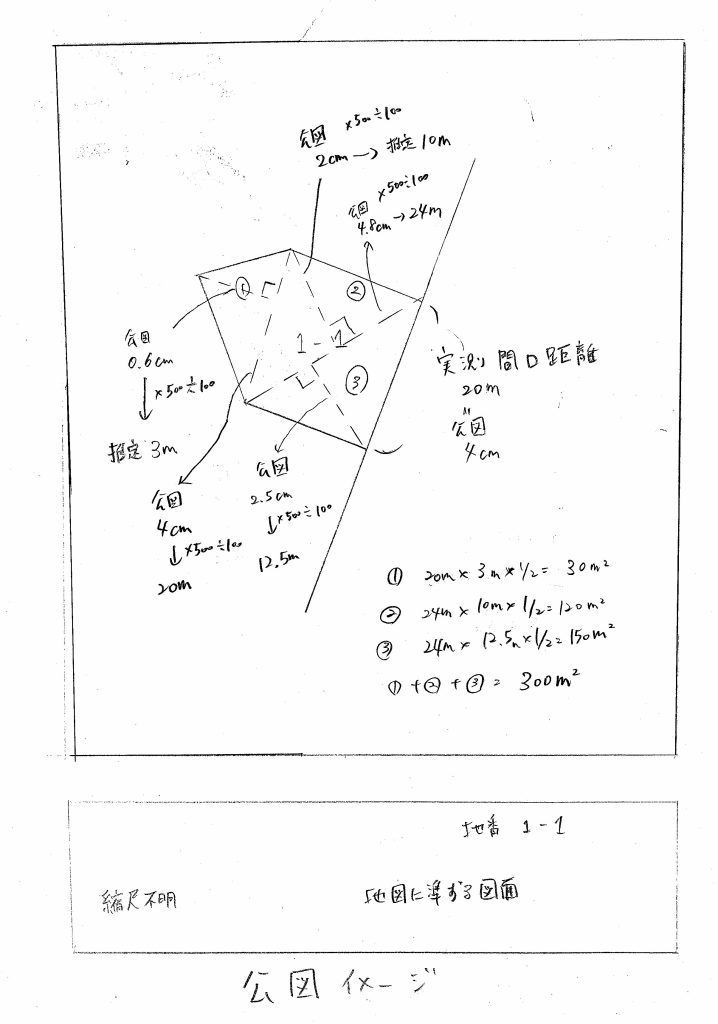
(図3)コピーした公図を作図して三斜面積計算を利用して地積を算出
下記において、公図から三斜面積計算を利用して地積を算出する手順を解説します。
・公図を取得し、作図用にコピーします。
・コピーした公図の対象土地を、すべて三角形に分割します。
・分割した三角形の底辺に対して垂直の高さを作図します。
・実測した間口距離に対応する公図の間口距離を測定すると縮尺割合のようなものが算出します。
・当該縮尺割合を利用して面積を計算します。
具体的な数値を用いて解説します。
・実測の間口距離が20mであり、公図等の間口距離の寸法が4cmであれば、4cm/2,000cmということで縮尺割合1/500となります。
・三角形①の公図での高さ寸法が0.6cmであれば500倍して100で割れば3mとなります。
・三角形①の公図での底辺寸法が4cmであれば500倍して100で割れば20mとなります。
・三角形②の公図での高さ寸法が2cmであれば500倍して100で割れば10mとなります。
・三角形②の公図での底辺寸法が4.8cmであれば500倍して100で割れば24mとなります。
・三角形③の公図での高さ寸法が2.5cmであれば500倍して100で割れば12.5mとなります。
・三角形①の面積は20m×3m×1/2=30㎡
・三角形②の面積は24m×10m×1/2=120㎡
・三角形③の面積は24m×12.5m×1/2=150㎡
・①+②+③=300㎡
となり、当該地番1-1の土地の地積は300㎡と算出されます。
地積測量図は既に三斜面積計算で面積が算出されている
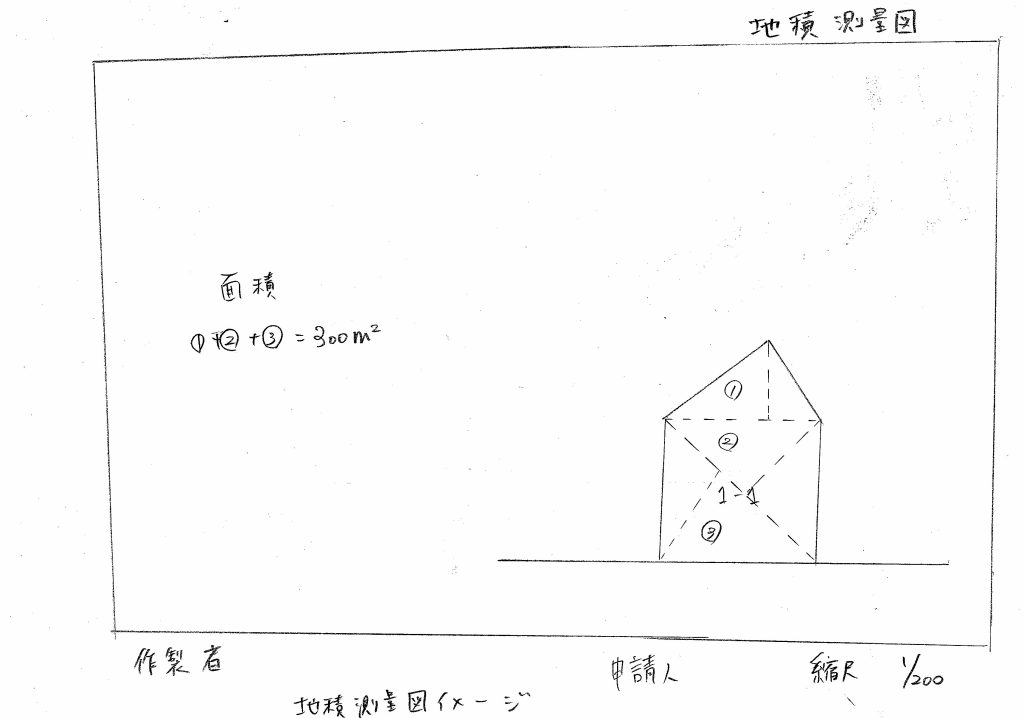
(図4)地積測量図のイメージ図
地積測量図は、まさに地積を測量した図であるため、作成者により、三斜面積計算を用いて地積が算出されております。また縮尺も明らかです。
建物図面は建物寸法及び縮尺が明らかであるため当該情報から三斜面積計算で地積を算出可能でしょう
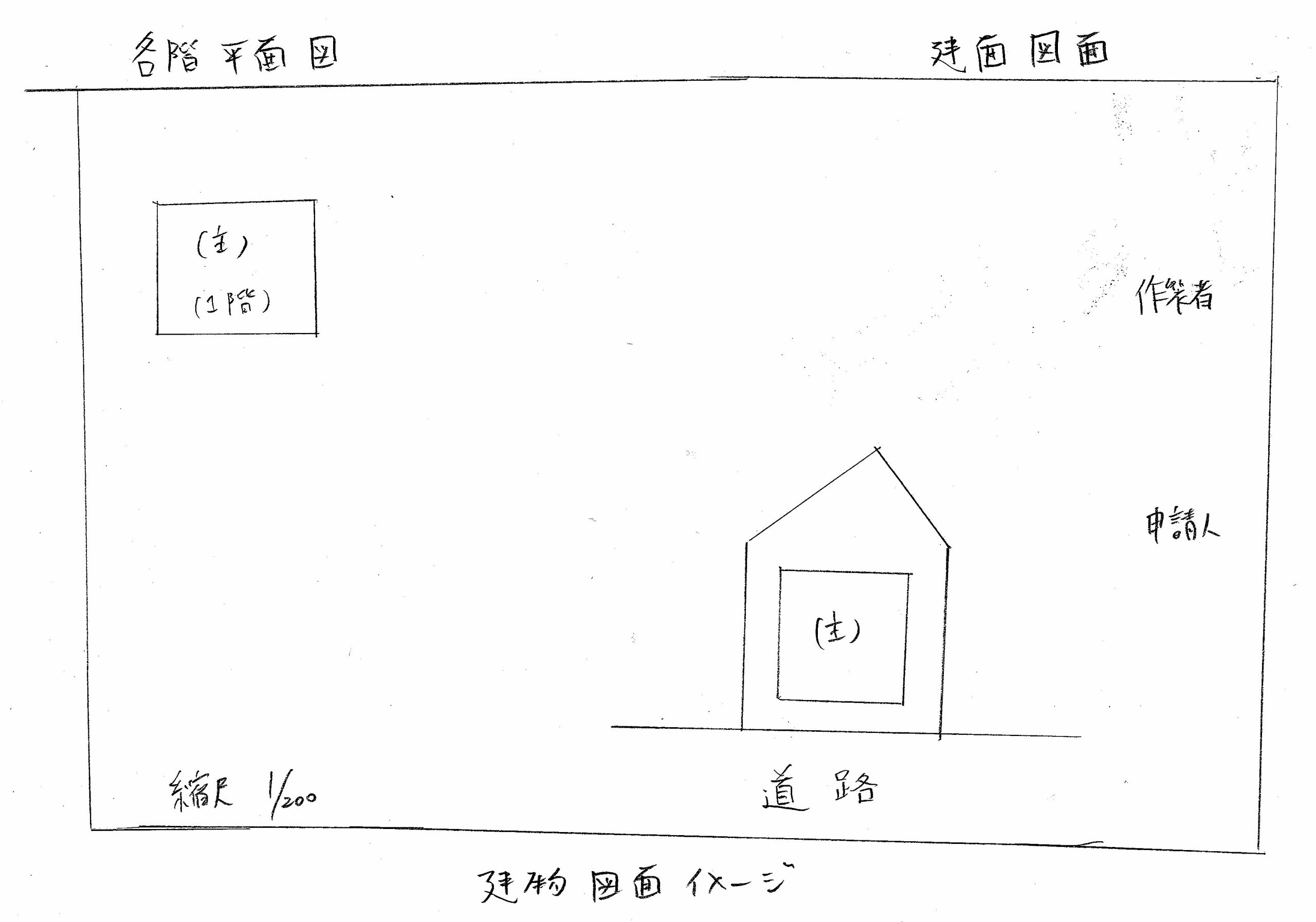
(図5)建物図面イメージ図
建物図面の主たる目的は、建物の寸法及び図面を明らかにすることです。しかし、建物は当然土地の上に建設されているため、土地も図面に描けれているケースが多く、寸法や縮尺が明らかであるため、土地の地積の算出に利用できることとなります。
ゼンリン住宅地図は公図と同じ取り扱いとなるでしょう
ゼンリン住宅地図は、公図と似ていることとなります。縮尺が明らかです。これらの情報を利用して三斜面積計算で地積を算出しましょう。
上記を理解すれば奥行距離も算出可能でしょう
このように、縮尺割合や寸法を利用すれば、奥行距離も机上で算出可能となります。
まとめ
・相続税における土地についての実測は、間口距離のみを必須としましょう。
・実測間口距離やその他資料を用いて机上で地積や奥行距離を算出可能です。